Graph Algorithms in Combat-TB-NeoDB

The neo4j-graph-algorithms library provides efficiently implemented, parallel versions of common graph algorithms for Neo4j, exposed as Cypher procedures.

In this section, we are going to use some of the centrality measures employed by Melak and Gakkahar to identify the most central proteins from protein–protein interaction network of Mycobacterium tuberculosis H37Rv which was retrieved from STRING by hypothesizing these proteins would be important to alter the function of the network (Melak and Gakkahar, 2014).

This is to illustrate the utility of graph analytics. It is not meant to replicate the work done in the above mentioned paper.

Centrality algorithms

Centrality algorithms are used to understand the roles of particular nodes in a graph and their impact on that network. They are useful because they identify the most important nodes and help us understand group dynamics such as credibility, accessibility, the speed at which things spread, and bridges between groups.

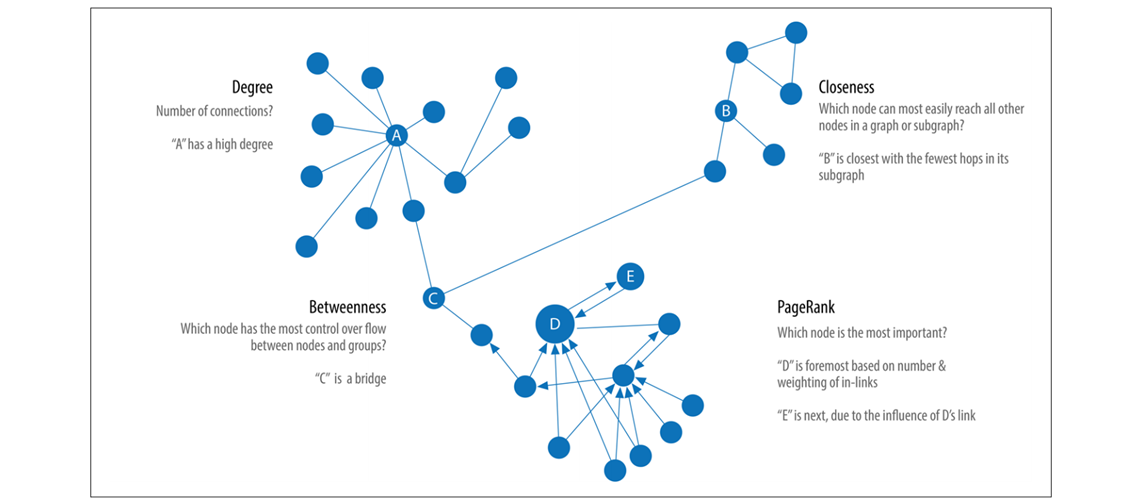Representative centrality algorithms (Source: Needham & Hodler, 2019)

Degree Centrality: Direct Importance

Degree centrality measures the number of incoming and outgoing relationships from a node.

The degree or connectivity of a Protein is the number of links connected to it, that is, the number of its interacting neighbors which is determined by counting the number of edges connected to a node.

The degree centrality measure ranks the potential of an individual node in the network based on its connectivity and it provides an indicator of its influence on the biological processes occurring in the organism, meaning that a protein with higher degree tends to contribute to several processes, and potentially be a key protein in the functioning of the system (Melak and Gakkahar, 2014).

The following query returns Proteins that have the most incoming interactors.

CALL algo.degree.stream("Protein", "INTERACTS_WITH", {direction: "incoming"})
YIELD nodeId, score
RETURN algo.asNode(nodeId).uniquename AS protein,
    algo.asNode(nodeId).name AS name,
    score AS incoming_interactors
ORDER BY incoming_interactors DESC

The following query returns Proteins that have the most outgoing interactors.

CALL algo.degree.stream("Protein", "INTERACTS_WITH", {direction: "outgoing"})
YIELD nodeId, score
RETURN algo.asNode(nodeId).uniquename AS protein,
    algo.asNode(nodeId).name AS name,
    score AS outgoing_interactors
ORDER BY outgoing_interactors DESC

Closeness Centrality: Average Farness (inverse distance)

Closeness centrality is a way of detecting nodes that are able to spread information very efficiently through a graph.

The closeness centrality of a node measures the centrality of a node based on how close it is to other nodes in the network. The smaller the total distance of a node to other nodes, the higher its closeness is. The distance between two nodes is defined as the length of the shortest path between them. We calculate closeness centrality measure for a node by inverting the sum of the distances from it to other nodes in the network.

The closeness measure is high for a Protein that is central since it has a shorter distance on average to other proteins.

CALL algo.closeness.stream("Protein", "INTERACTS_WITH")
YIELD nodeId, centrality
RETURN algo.asNode(nodeId).uniquename AS protein, centrality
ORDER BY centrality DESC
LIMIT 20;

Betweenness Centrality: Shortest (weighted) Path

Betweenness centrality is a way of detecting the amount of influence a node has over the flow of information in a graph. It is often used to find nodes that serve as a bridge from one part of a graph to another.

The betweenness centrality of a Protein in a functional network is a metric that expresses its influence relative to other proteins within the network. It is based on the proportion of shortest paths between other proteins passing through the protein target and shows the importance of a protein for the transmission of information between other proteins in the network. This metric provides an indication of the number of pair-wise proteins connected indirectly by the protein target through their direct functional connections (Melak and Gakkahar, 2014).

Proteins with higher rank of betweenness are expected to ensure the connectivity between proteins in the functional network and are able to bridge or disconnect connected components.

CALL algo.betweenness.stream("Protein", "INTERACTS_WITH", {direction:'out'})
YIELD nodeId, centrality
MATCH (protein:Protein) WHERE id(protein) = nodeId
RETURN protein.uniquename AS protein,centrality
ORDER BY centrality DESC;

Transitive Importance

Eigenvector Centrality

Like degree centrality, the Eigenvector Centrality algorithm measures a node’s transitive influence by counting the number of links it has to other nodes within the network. However, it goes a step further by also taking into account how well connected a node is, and how many links their connections have, and so on through the network.

A high Eigenvector centrality score indicates a strong influence over other nodes in the network. It is useful because it indicates not just direct influence, but also implies influence over nodes more than one ‘hop’ away.

The following will run the algorithm and stream results normalized using max (divide all scores by the maximum score).

CALL algo.eigenvector.stream("Protein", "INTERACTS_WITH", {normalization: "max"})
YIELD nodeId, score
RETURN algo.asNode(nodeId).uniquename AS protein,score
ORDER BY score DESC

PageRank

PageRank, a variant of Eigenvector Centrality, is an algorithm that measures the transitive influence or connectivity of nodes.

It uses links between nodes as a measure of importance. Each node in a network is assigned a score based upon its number of incoming links (its ‘indegree’). These links are also weighted depending on the relative score of its originating node.

Nodes with many incoming links are influential, and nodes to which they are connected share some of that influence.

Like Eigenvector centrality, PageRank can help uncover influential or important nodes whose reach extends beyond just their direct connections.

We can use this algorithm to find important Proteins based not only on whether they INTERACT_WITH a lots of Proteins, but whether those Proteins are themselves important.

The following will run the algorithm and stream results.

CALL algo.pageRank.stream("Protein", "INTERACTS_WITH", {iterations:20, dampingFactor:0.85})
YIELD nodeId, score
RETURN algo.asNode(nodeId).uniquename AS protein,score
ORDER BY score DESC

Community detection algorithms

Community detection is a very active field in complex networks analysis, consisting in identifying groups of nodes more densely interconnected relatively to the rest of the network.

Triangle Counting / Clustering Coefficient

Triangle counting is a community detection graph algorithm that is used to determine the number of triangles passing through each node in the graph. A triangle is a set of three nodes, where each node has a relationship to all other nodes.

A clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together.

The following will count the number of triangles that a node (Protein) is member of, and return a stream with the UniProt ID and triangleCount:

CALL algo.triangleCount.stream('Protein', 'INTERACTS_WITH', {concurrency:4})
YIELD nodeId, triangles, coefficient
RETURN algo.asNode(nodeId).uniquename AS UniProtID, triangles, coefficient
ORDER BY coefficient DESC

The following will count the number of triangles that a node (Protein) is member of, and write it back. It will return the total triangle count and average clustering coefficient of the interaction network.

CALL algo.triangleCount('Protein', 'INTERACTS_WITH',
  {concurrency:4, write:true, writeProperty:'triangles',clusteringCoefficientProperty:'coefficient'})
YIELD nodeCount, triangleCount, averageClusteringCoefficient;

Result:

╒═══════════╤═══════════════╤══════════════════════════════╕
│"nodeCount"│"triangleCount"│"averageClusteringCoefficient"│
╞═══════════╪═══════════════╪══════════════════════════════╡
│3984       │104198         │0.36405616179922706           │
└───────────┴───────────────┴──────────────────────────────┘

The average clustering coefficient of the Protein-Protein interaction network, with 3984 Proteins, is 0.36405616179922706.